Linear mixed model
Overview
linear_mixed_model.m fits one-way or two-way linear mixed models to data with an optional grouping variable.
linear_mixed_model.m has an option to create simple swarmcharts that illustrate the data but the plots do not show statistical effects.
fig_jitter.m can be used in combination with linear_mixed_model.m to make publication-quality figures.
One-way
Without a grouping variable, a linear-mixed model is similar to a standard ANOVA.
Code
function linear_mixed_model_one_way
% Create data
n_f1 = 3;
n = 4;
noise = 0.3;
for i = 1 : n_f1
vi = (i-1)*n+(1:n);
y(vi) = i;
f1(vi) = repmat(sprintf("%.i", i), [1, n]);
end
% Add some jitter, resetting randumber generator for consistency
rng(1)
y = y + noise * (rand(size(y)) - 0.5);
% Form the table
t = table(y', f1', VariableNames = ["y", "Block"]);
% Run the stats test
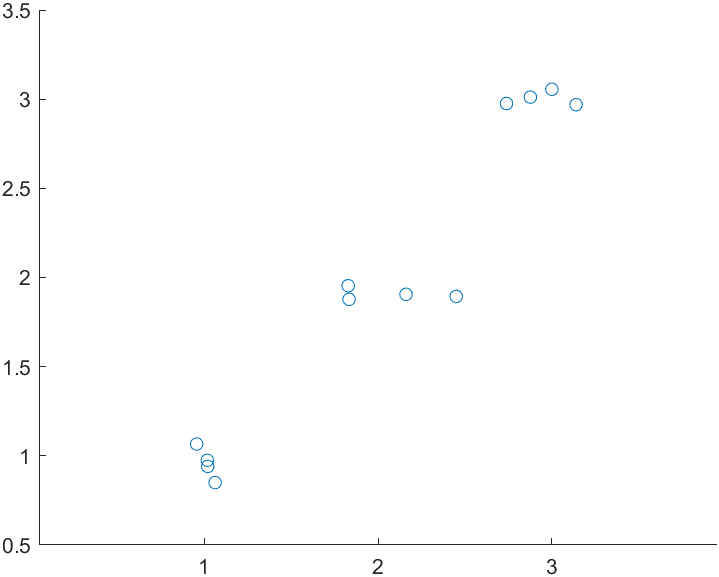
stats = linear_mixed_model(t, "y", "Block", figure_handle = 1)
me = stats.main_effects
pc = stats.post_hoc
ms = stats.model_string
mes = stats.main_effects_string
Output
>> linear_mixed_model_one_way
Warning: Ignoring 'CovariancePattern' parameter since the model has no random effects.
> In classreg.regr.LinearLikeMixedModel.validateCovariancePattern (line 1617)
In LinearMixedModel.fit (line 2392)
In fitlme (line 233)
In linear_mixed_model (line 39)
In demo_statistics_linear_mixed_model_one_way (line 20)
Warning: Ignoring 'CovariancePattern' parameter since the model has no random effects.
> In classreg.regr.LinearLikeMixedModel.validateCovariancePattern (line 1617)
In LinearMixedModel.fit (line 2392)
In fitlme (line 233)
In linear_mixed_model (line 45)
In demo_statistics_linear_mixed_model_one_way (line 20)
stats =
struct with fields:
main_effects: [1×5 classreg.regr.lmeutils.titleddataset]
post_hoc: [3×7 table]
model_string: "y ~ 1 + Block"
main_effects_string: "Block: p < 0.001"
me =
ANOVA marginal tests: DFMethod = 'Satterthwaite'
Term FStat DF1 DF2 pValue
{'Block'} 1183 2 9 1.2696e-11
pc =
3×7 table
varname_1 varname_2 p_raw F df1 df2 p_corrected
_________ _________ __________ ______ ___ ___ ___________
"1" "3" 3.3142e-12 2362 1 9 9.9427e-12
"3" "2" 8.802e-10 677.41 1 9 1.7604e-09
"1" "2" 3.1151e-09 509.54 1 9 3.1151e-09
ms =
"y ~ 1 + Block"
mes =
"Block: p < 0.001"
>>
 )
)
Comments
-
MATLAB prints a warning because
linear_mixed_model.mis called using an option that only makes sense if there is a grouping variable. You can ignore this warning for the demo but you should also realize that you are running a test that could be done more simply using a standard one-way ANOVA. -
The post-hoc table is ordered by the p_corrected column which uses a Holm-Bonferroni approach.
-
The plot is ultra-simple and is intended mainly to help visualize the data.
One-way with grouping
This example builds on the last but adds a grouping variable
Code
linear_mixed_model_one_way_with_grouping.m
function linear_mixed_model_one_way_with_grouping
% Create data
n_f1 = 3;
n = 10;
noise = 0.6;
for i = 1 : n_f1
vi = (i-1)*n+(1:n);
y(vi) = i;
f1(vi) = repmat(sprintf("%.i", i), [1, n]);
end
% Add some jitter, resetting randumber generator for consistency
rng(1)
y = y + noise * (rand(size(y)) - 0.5);
% Add a grouping variable
g = randi(5, size(y));
% Form the table
t = table(y', f1', g', VariableNames = ["y", "Block", "ID"]);
% Run the stats test
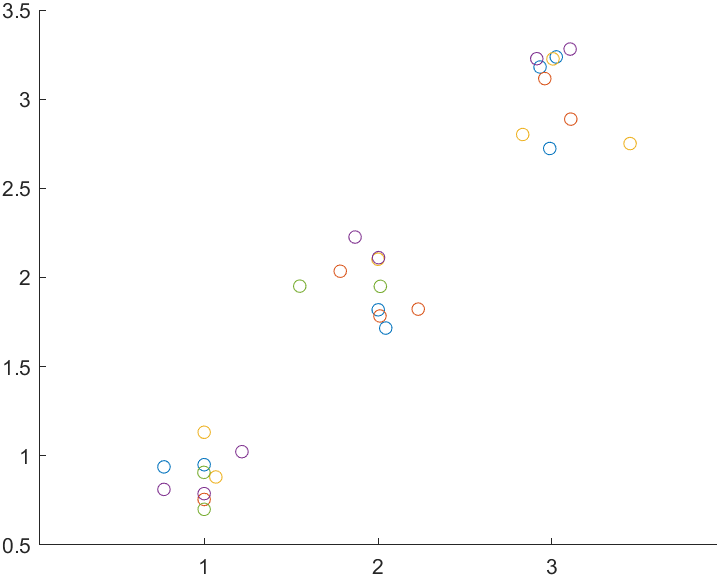
stats = linear_mixed_model(t, "y", "Block", ...
grouping_label = "ID", ...
figure_handle = 1)
% Expand the output
me = stats.main_effects
pc = stats.post_hoc
ms = stats.model_string
mes = stats.main_effects_string
% Save the figure
exportgraphics(gcf, 'one_way_with_grouping.png')
Output
stats =
struct with fields:
main_effects: [1×5 classreg.regr.lmeutils.titleddataset]
post_hoc: [3×7 table]
model_string: "y ~ 1 + Block + (1 | ID)"
main_effects_string: "Block: p < 0.001"
me =
ANOVA marginal tests: DFMethod = 'Satterthwaite'
Term FStat DF1 DF2 pValue
{'Block'} 376.18 2 25.58 1.0756e-19
pc =
3×7 table
varname_1 varname_2 p_raw F df1 df2 p_corrected
_________ _________ __________ ______ ___ ______ ___________
"1" "3" 1.5367e-20 752.35 1 25.665 4.61e-20
"3" "2" 1.6998e-13 190.73 1 26.048 3.3997e-13
"1" "2" 4.2411e-13 185.55 1 25.104 4.2411e-13
ms =
"y ~ 1 + Block + (1 | ID)"
mes =
"Block: p < 0.001"
 )
)
Comments
-
The colors in the plot show group membership.
-
If you run this test without grouping (not shown here), you will get almost the same p-values. This is because, in this example, the data values are randomly distributed within each group.
- If you want to see grouping changing the p-values, you can adjust the code so that the group membership influences the data values. One way is to adjust the group section to
% Add a grouping variable
g = randi(5, size(y));
% Adjust data based on group
y = y + 0.2 * g
Two-way
This is the first example of a 2-way test.
Code
function linear_mixed_model_two_way
% Create data
n_f1 = 3;
n_f2 = 2;
n = 10;
noise = 1;
for i = 1 : n_f1
for j = 1 : n_f2
vi = (i-1)*(n_f2*n) + (j-1)*n + (1:n);
y(vi) = i * j;
f1(vi) = repmat(sprintf("%i", i), [1, n]);
f2(vi) = repmat(sprintf("%c", j+64), [1, n]);
end
end
% Add some jitter, resetting randumber generator for consistency
rng(1)
y = y + noise * (rand(size(y)) - 0.5);
% Form the table
t = table(y', f1', f2', VariableNames = ["y", "Block", "City"])
% Run the stats test
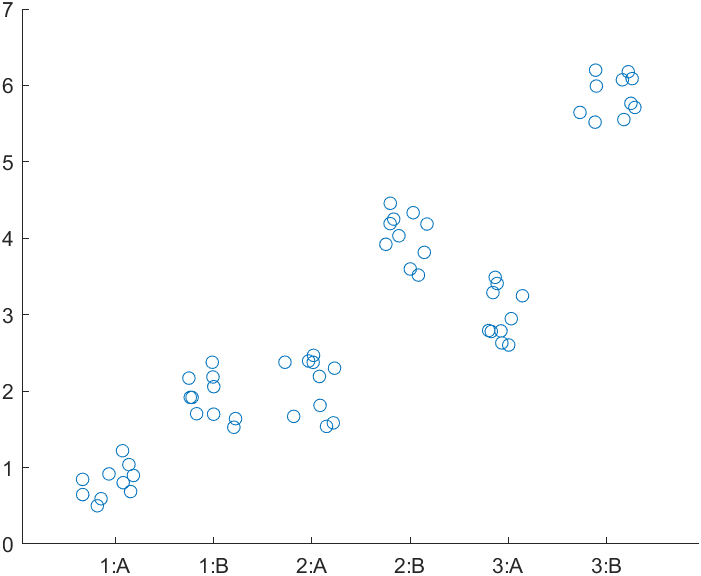
stats = linear_mixed_model(t, "y", "Block", ...
f2_label = "City", ...
figure_handle = 1)
% Expand the output
me = stats.main_effects
pc = stats.post_hoc
ms = stats.model_string
mes = stats.main_effects_string
% Save the figure
exportgraphics(gcf, 'two_way.png')
Output
stats =
struct with fields:
main_effects: [3×5 classreg.regr.lmeutils.titleddataset]
post_hoc: [9×7 table]
model_string: "y ~ 1 + Block + City + (Block * City)"
main_effects_string: "Block: p < 0.001↵City: p < 0.001↵Block * City: p < 0.001"
me =
ANOVA marginal tests: DFMethod = 'Satterthwaite'
Term FStat DF1 DF2 pValue
{'Block' } 524.29 2 54 4.2612e-36
{'City' } 652.87 1 54 7.8137e-32
{'Block:City'} 43.499 2 54 5.5702e-12
pc =
9×7 table
varname_1 varname_2 p_raw F df1 df2 p_corrected
_________ _________ __________ ______ ___ ___ ___________
"1:B" "3:B" 6.0026e-35 867.6 1 54 5.4024e-34
"3:A" "3:B" 4.5596e-28 458.98 1 54 3.6477e-27
"1:A" "3:A" 1.815e-22 264.62 1 54 1.2705e-21
"1:B" "2:B" 8.2013e-22 247.37 1 54 4.9208e-21
"2:A" "2:B" 2.1732e-20 213.06 1 54 1.0866e-19
"2:B" "3:B" 2.9987e-19 188.43 1 54 1.1995e-18
"1:A" "2:A" 6.5636e-13 87.745 1 54 1.9691e-12
"1:A" "1:B" 4.1152e-11 67.828 1 54 8.2303e-11
"2:A" "3:A" 5.9925e-09 47.607 1 54 5.9925e-09
ms =
"y ~ 1 + Block + City + (Block * City)"
mes =
"Block: p < 0.001
City: p < 0.001
Block * City: p < 0.001"
Comments
- Note how increasing the combinations substantially increases the number of post-hoc tests
Two-way with grouping
Now we can add a grouping variable to the design
Code
linear_mixed_model_two_way_with_grouping.m
% Create data
n_f1 = 3;
n_f2 = 2;
n = 10;
noise = 0.5;
for i = 1 : n_f1
for j = 1 : n_f2
vi = (i-1)*(n_f2*n) + (j-1)*n + (1:n);
y(vi) = 1 + 0.2*i + 0.2*j;
f1(vi) = repmat(sprintf("%i", i), [1, n]);
f2(vi) = repmat(sprintf("%c", j+64), [1, n]);
end
end
% Add some jitter, resetting randumber generator for consistency
rng(1)
y = y + noise * (rand(size(y)) - 0.5);
% Add a grouping variable
g = randi(5,size(y));
% Form the table
t = table(y', f1', f2', g', ...
VariableNames = ["y", "Block", "City", "ID"]);
% Run the stats test
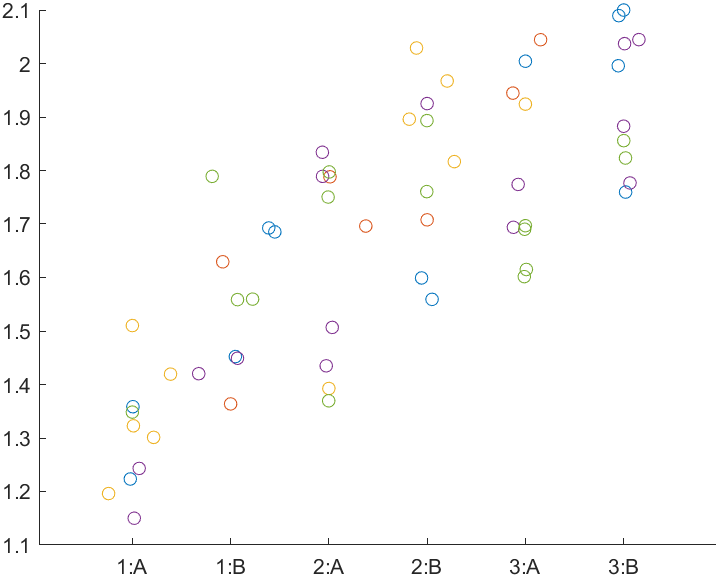
stats = linear_mixed_model(t, "y", "Block", ...
f2_label = "City", ...
grouping_label = "ID", ...
figure_handle = 1);
% Expand the output
me = stats.main_effects
pc = stats.post_hoc
ms = stats.model_string
mes = stats.main_effects_string
% Save the figure
exportgraphics(gcf, 'two_way_with_grouping.png')
Output
me =
ANOVA marginal tests: DFMethod = 'Satterthwaite'
Term FStat DF1 DF2 pValue
{'Block' } 13.83 2 54 1.4134e-05
{'City' } 5.3865 1 54 0.024098
{'Block:City'} 0.75282 2 54 0.47591
pc =
9×7 table
varname_1 varname_2 p_raw F df1 df2 p_corrected
_________ _________ __________ ________ ___ ___ ___________
"1:A" "3:A" 6.1824e-05 18.881 1 54 0.00055642
"1:A" "2:A" 0.0012499 11.603 1 54 0.0099991
"1:B" "3:B" 0.011074 6.9218 1 54 0.077521
"1:A" "1:B" 0.02691 5.175 1 54 0.13455
"1:B" "2:B" 0.024388 5.3635 1 54 0.14633
"2:B" "3:B" 0.75397 0.099229 1 54 0.75397
"2:A" "2:B" 0.24142 1.403 1 54 0.96567
"2:A" "3:A" 0.35197 0.88152 1 54 1.0559
"3:A" "3:B" 0.5774 0.31425 1 54 1.1548
ms =
"y ~ 1 + Block + City + (Block * City)"
mes =
"Block: p < 0.001
City: p = 0.024
Block * City: p = 0.476"
Comments
- You might be puzzled how some of the p_corrected values now exceed 1. This is a consequence of the Holm-Bonferroni algorithm which works as follows
- Order the m post-hoc tests in ascending p-order
- Correct the lowest p-value by multiplying it by m
- Correct the next lowest p-value by multiplying it by m-1
- Continue until you multiply the highest p-value by 1
- Now look at the table
- “2:B” v “3:B” has the same p_raw and p_corrected values. It also has the highest p_raw value, so its p_corrected was obtained by multipling by 1
- Values with p_corrected > 1 were obtained by multiplying p_raw < 1 by m > 1. For example, for “3:A” v “3:B”, p_corrected = 2 * p_raw