Link Search Menu Expand Document
MATMyoSim

Pendulum

Overview

This set of demos connects a MATMyoSim model to a mechanical system - in this case, a simple pendulum. The intent is to show how the pendulum system and the MATMyoSim model interact. That is, the pendulum perturbs the muscle model, and model influences the pendulum.

Assumptions

The system is as shown.

The pendulum is mimicked as a mass m of length L. Small angles are assumed so that when the pendulum is displaced to a position x, the horizontal force acting on the pendulum is m g sin(theta) which is approximately m g x / L.

If the pendulum is subject to viscous damping eta, the movement of the pendulum is given by

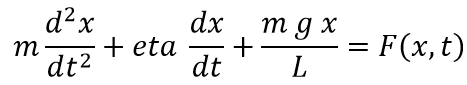
where F(x,t) is the force from the MATMyoSim model. This can be transformed into two coupled first-order equations by defining a new variable y = dx/dt.

Calculations

The simulations are started with the pendulum’s position and velocity defined by a vector of initial conditions. The calculations then iterate through a series of time-steps, each of which advances the simulation by $\Delta$t.

During each time-step,

  • the movement of the pendulum $\Delta$x is calculated by integrating the differential equations for the pendulum.
  • the MATMyoSim model is updated with:
    • the displacement `hsl_scaling_factor * $\Delta$x
    • the Ca2+ concentration for the time-step

This yields an updated MATMyoSim force the next time-step.

This calculation is performed by the function implement_pendulum_protocol() in the simulation class. The behavior of the pendulum is defined by the function pend_derivs

function dy = pend_derivs(t, yy, pend, f)
    dy = NaN*ones(2,1);
    dy(1)= yy(2);
    dy(2) = (-pend.force_scaling_factor * f / pend.m) - (pend.eta*yy(2) / pend.m) - ...
                (pend.g * yy(1) / pend.L);
end

This approach could be modified in future work to simulate different systems.

Scaling factors

Parameter Comment
hsl_scaling_factor the displacement of the MATMyoSim model in nm if the pendulum moves 1 m
force_scaling_factor the force applied to the pendulum in N is the product of force_scaling_factor and the stress (force per unit area) predicted by MATMyoSim

Pendulum file

The pendulum system is defined by a JSON file. Here is an example.

{
    "pendulum":
    {
        "m": 10,
        "L": 0.25,
        "g": 9.81,
        "eta": 0,
        "hsl_scaling_factor": 500,
        "force_scaling_factor": 1e-3,
        "initial_conditions": [0.05, 0]
    }
}

The two values in the initial conditions array define the starting position (in m) and velocity (in m s-1) respectively.

See the demos for examples.

Table of contents