Ramp 3 demonstration

This demo shows how to run a simulation of a single sarcomere subjected to a ramp, hold, and then release protocol.

It builds on ramp_1 by adding in a population of cross-bridges that cycle but do not generate force.

Instructions

Launch MATLAB.
Change directory to the MATMyoSim\code\demos\ramps\ramp_3 folder in MATLAB.
Open demo_ramp_3.m.
Press F5 to run the demo.

Code

function demo_ramp_3
% Function illustrates how to run a simulation of a single-half-sarcomere
% with a linear passive elastic component and cycling cross-bridges
% that do not generate active force

% Variables
protocol_file_string = 'ramp_3_protocol.txt';
model_parameters_json_file_string = 'ramp_3_parameters.json';
options_file_string = 'ramp_3_options.json';
model_output_file_string = '..\..\temp\ramp_3_output.myo';

% Make sure the path allows us to find the right files
addpath(genpath('..\..\..\..\code'));

% Run a simulation
sim_output = simulation_driver( ...
    'simulation_protocol_file_string', protocol_file_string, ...
    'model_json_file_string', model_parameters_json_file_string, ...
    'options_json_file_string', options_file_string, ...
    'output_file_string', model_output_file_string);

% Load it back up and display to show how that can be done
sim = load(model_output_file_string,'-mat')
sim_output = sim.sim_output

figure(2);
clf;
subplot(2,1,1);
plot(sim_output.time_s,sim_output.muscle_force,'b-');
ylabel('Force (N m^{-2})');
subplot(2,1,2);
plot(sim_output.time_s,sim_output.hs_length,'b-');
ylabel('Half-sarcomere length (nm)');
xlabel('Time (s)');

Model

The model is defined in repo\code\demos\ramps\ramp_3\ramp_3_parameters.json.

{
    "MyoSim_model":
    {
        "muscle_props":
        {
            "no_of_half_sarcomeres": 1,
            "series_k_linear": 0
        },
        "hs_props":
        {
            "kinetic_scheme": "3state_with_SRX",
            "hs_length": 1300,
            "myofilaments":
            {
                "bin_min": -10,
                "bin_max": 10,
                "bin_width": 0.5,
                "thick_filament_length": 815,
                "thin_filament_length": 1120,
                "bare_zone_length": 80,
                "k_falloff": 0
            },
            "parameters":
            {
                "k_1": 10,
                "k_force": 0.0,
                "k_2": 100,
                "k_3": 1,
                "k_4_0": 20,
                "k_4_1": 0.1,
                "k_cb": 0.001,
                "x_ps": 0,
                "k_on": 6e7,
                "k_off": 200,
                "k_coop": 10,
                "passive_force_mode": "linear",
                "passive_hsl_slack": 1250,
                "passive_k_linear": 100,
                "compliance_factor": 0.5,
                "cb_number_density": 6.9e16,
                "k_boltzmann": 1.38e-23,
                "temperature": 288,
                "max_rate": 5000
            }
        }
    }
}

Output

Simulation output

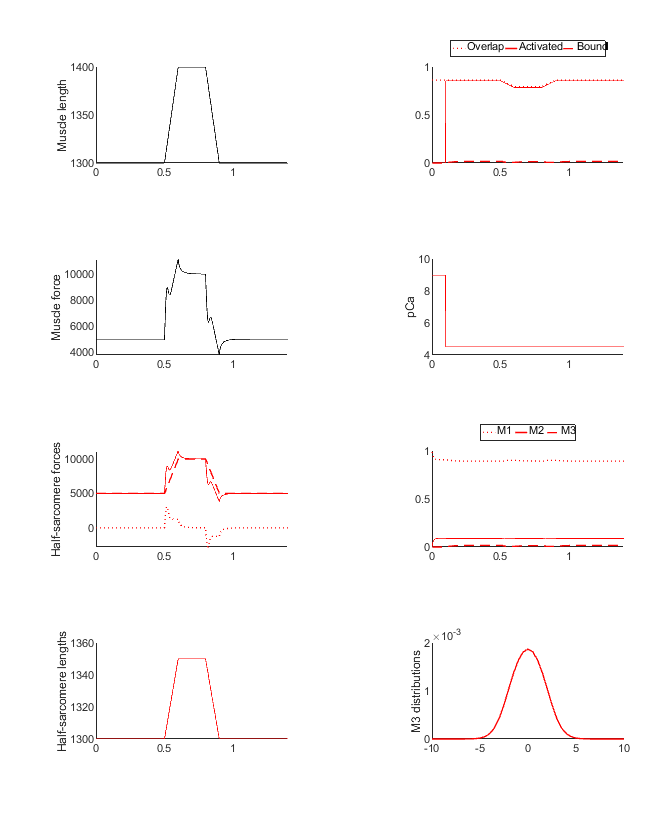
Replotted from output file 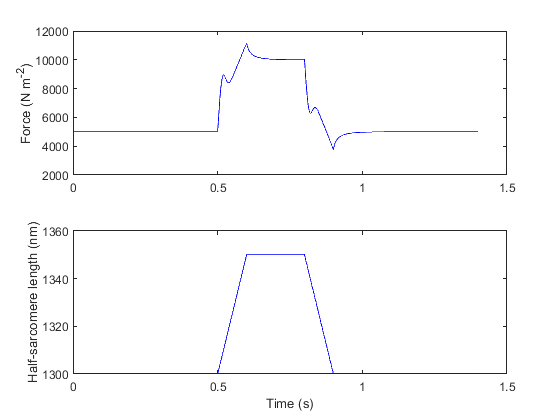Replotted output

Comments

If you look at the json model structure, you will see that

the passive component is 10 times stiffer than it was in ramp_1
- passive_k_linear is 100 N m^-2 nm^-1 instead of 10 N m^-2 nm^-1)
k_3 = 1 s^-1 nm^-1
- As shown in 3state_with_SRX this allows myosin heads to attach to the thin filament
x_ps = 0 nm
- Thus the attached cross-bridges do not generate active force. They do however link the filaments. If the filaments move relative to each other, the attached cross-bridges generate a drag.

The force produced by this model is thus the sum of the linear passive elastic force and a drag from attached cross-bridges. The cycling kinetics of the heads mean that the cross-bridges produce a visco-elastic drag.