Lattice equations
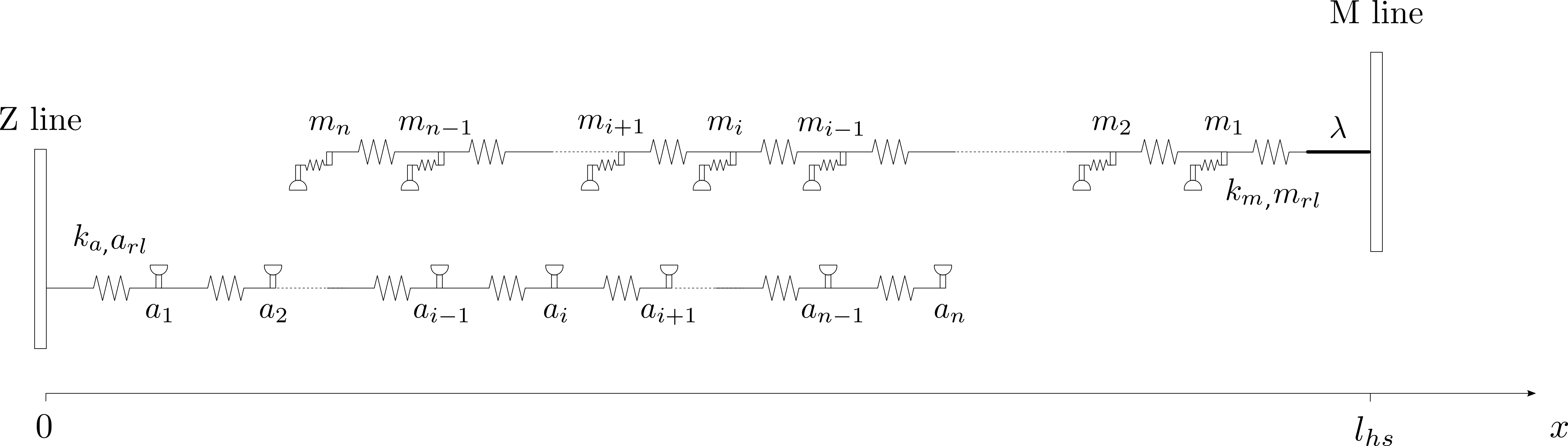
In FiberSim, the thick and thin filaments within each half-sarcomere are mimicked as a series of nodes joined by compliant springs. The nodes on the thin filament represent actin monomers. The nodes on the thick filaments represent myosin crowns.
The force in the half-sarcomere is calculated from the extension of the springs nearest the Z-line. The force in each filaments is obtained from Hooke’s law (force = stiffness * extension). The force in the half-sarcomere is obtained by summing the forces in each thin filament.
It follows that determining the position of each node is a pivotal operation in FiberSim. This is achieved by assuming that forces are balanced at each node at each time-step.
This page explains the equations that goven force-balance. The procedures used to calculate the node positions are described at KX=F.
Actin filaments
Thin filaments are composed of nodes joined by linear springs of stiffness \(k_{a}\) with a resting length \(a_{rl}\). If the position of the \(i^{th}\) node along an x-axis is noted \(a_i\), then the force-balance equations for the thin filament can be written as:
\[2 \, k_a \, a_1 - k_a \, a_2 = 0\] \[- k_a \, a_{i-1} + 2 \, k_a \, a_i - k_a \, a_{i+1} = 0 \,\,\, \text{for} \, 1 \lt i \lt n\] \[-k_a \, a_{n-1} + k_a \, a_n = k_a \, a_{rl}\]Myosin filaments
Thick filaments are composed of nodes joined by linear springs of stiffness \(k_{m}\) with a resting length \(m_{rl}\). A rigid link of length \(\lambda\) connects the thick filament to the M-line. If the position of the \(i^{th}\) node along an x-axis is noted \(m_i\), and the half-sarcomere length is noted \(l_{hs}\), then the force-balance equations for the thick filament can be written as:
\[2 \, k_m \, m_1 - k_m \, m_2 = k_m \, (l_{hs}- \lambda)\] \[- k_m \, m_{i-1} + 2 \, k_m \, m_i - k_m \, m_{i+1} = 0 \,\,\, \text{for} \, 1 \lt i \lt n\] \[k_m \, m_{n-1} - k_m \, m_n = -k_m \, m_{rl}\]The system of equations for the thin and thick filament can be written in matrix form:
\[K x = F\]where \(K\) is a matrix containing the springs stiffness, \(x\) is a vector containing the positions of the actin and myosin nodes (\(a_i\) and \(m_i\), respectively) and \(F\) is a vector containing the constant terms (independent of nodes positions). \(K\) is a tridiagonal matrix:
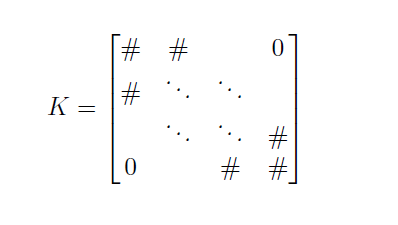
and numerical methods exist to solve \(Kx=F\) for \(x\).
Cross-bridge links
Myosin heads located at the thick filament nodes can attach to neighboring binding sites at the thin filament nodes, thus affecting the filament lattice framework.
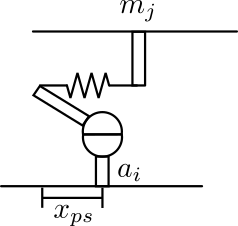
A cross-bridge located at the \(j^{th}\) thick filament node which attaches to the \(i^{th}\) node of the thin filament generates a force \(f_{cb}\) given by:
\[f_{cb} = k_{cb} \, (m_j - a_i + x_{ps})\]where \(k_{cb}\) is the cross-bridge spring stiffness and \(x_{ps}\) is the crossbridge extension when deploying the power stroke.
This additional force on the filaments should be added to the force-balance equations :
\[- k_a \, a_{i-1} + 2 \, k_a \, a_i - k_a \, a_{i+1} \, \color{red}{+ \, k_{cb} \, a_i - k_{cb} \, m_j} = \color{blue}{k_{cb} \, x_{ps}}\] \[- k_m \, m_{j-1} + 2 \, k_m \, m_j - k_m \, m_{j+1} \, \color{red}{- \, k_{cb} \, a_i + k_{cb} \, m_j} = \color{blue}{-k_{cb} \, x_{ps}}\]The terms in red will add non-tridiagonal, opposite elements to the \(K\) matrix:

while the blue terms will contribute to the \(F\) vector.
Cross-bridge linking toughens the numerical solving of \(K x = F\), which notably requires an iterative procedure to find a solution \(x\) that satisfies a certain precision.
Titin
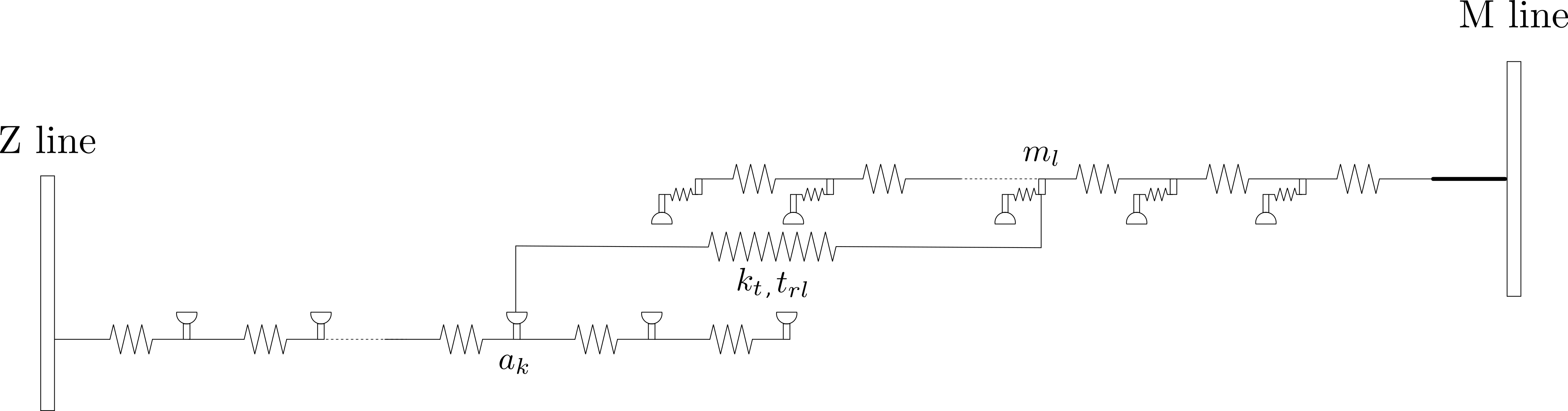
Titin is responsible for the passive force developing within the half-sarcomere when it is stretched, and for the recoil force when it is shortened. In the model, it is assumed that titin is a linear spring of stiffness \(k_t\) and rest length \(t_{rl}\). This spring is attached at both ends, on a particular thick and thin filament node respectively. Similar to crossbridge links, titin contributes \(f_{t}\) to the force-balance equation.
The default behavior is:
\[f_{t} = k_{t} \, (m_l - a_k)\]If t_passive_mode is defined as exponential, the equation is modified to:
Myosin Binding Protein C
Myosin Binding Protein C (MyBP-C) is a striated muscle contracting protein. It is associated with the thick filaments and located near the center of the sarcomere, in the C-zones.
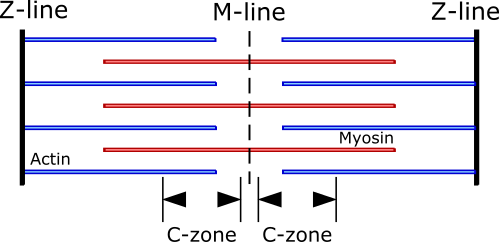
This protein interacts both with myosin and actin and is a modulator of cardiac contractility. In the model, MyBPC can attach to an actin binding site and act as a “non-force-generating cross-bridge link” (meaning it cannot undergo a power stroke). Such C-links contribute to the force-balance equations:
\[f_{pc} = k_{pc} \, (m_j - a_i)\]where \(k_{pc}\) is the C-link stiffness.